MENGGAMBAR GRAFIK FUNGSI DENGAN TURUNAN PERTAMA DAN TURUNAN KEDUA

By. Davin Ilham Wijaya (10)

XI IPS 2

Bismillahirrahmanirrahiim......yuk kita mulai dengan mengetahui

Langkah-langkah menggambar grafik fungsi menggunakan turunan :

1. Menentukan titik potong dengan sumbu-sumbu koordinat (sumbu x dan sumbu y)

    Titik potong sumbu x, subsitusi y = 0

    Titik potong sumbu y, subsitusi x = 0

2. Menentukan titik-titik stasioner dan jenisnya (titik balik minimun, titik balik maksimum 

    dan titik belok)

3. Menentukan titik bantuan lainnya agar membuat grafiknya lebih mudah atau bisa juga

   secara umum menentukan nilai y untuk  besar x positif dan  besar x negatif.

CONTOH SOAL :

Diketahui persamaan y = f(x) = 3x – x 3 

tentukan : a. Tentukan titik potong dngan sumbu x dan sumbu y. 

                 b. Nilai stasioner dan titik stasioner. 

                 c. Nilai y untuk x besar positif dan untuk x besar negative. 

                 d. Titik Bantu 

                 e. Gambarlah grafiknya

JAWAB :

a. i. Grafik memotong sumbu x, bila y = 0. 

       Y = 0 = 3x – x³

        ↔ 0 = x (3 – x 2 )

        ↔ 0 = x (√ 3 - x ) (√ 3 + x) 

       Titik potong sumbu x adalah (0,0), ( √3 ,0), (-√ 3 ,0) 

    ii. memotong sumbu y, jika x = 0 

        y = 3x – x³ 

        y = 3.0 - 0³ 

        y = 0

       titik potong sumbu y adalah (0,0) 

b. Syarat stasioner adalah : f’ (x) = 0 

    f’ (x) = 3 – 3x²

   ↔ 3 (1 - x ² ) 

   ↔ 3 (1 – x) (1 + x) 

       x = 1, x = -1  

   untuk x = 1, f(1) = 3(1) – (1)3 = 2 

             x = -1, f(-1) = 3(-1) – (-1)3 = -2

   nilai stasionernya : y = 2 dan y = -2

   titik stasioner : (1,2) dan (-1,-2) 

c. y = 3x – x 2 , untuk nilai x besar maka bilangan 3 dapat diabaikan terhadap x, 

   sehingga y = -x 3 . Jika x besar positif maka y = besar negatif dan jika x besar negatif 

   maka y besar positif

Soal Pilhan Ganda :

1. Diketahui grafik fungsi 

$y_1=5\sin x$ dan $y_2=\sin 5x$. Pernyataan berikut yang benar adalah $\cdots \cdot$
A. periode $y_1$ = periode $y_2$
B. amplitudo $y_1$ = amplitudo $y_2$
C. periode $y_1=\frac{1}{5}$ kali periode $y_2$
D. amplitudo $y_1=\frac{1}{5}$ kali amplitudo $y_2$
E. amplitudo $y_1=5$ kali amplitudo $y_2$

Pembahasan

Bentuk umum fungsi sinus tersebut adalah $y=a\sin kx$.
Periode:
Periode $y_1=5\sin x$ dengan $k=1$ adalah $P_1=\frac{{360}^{\circ }}{1}={360}^{\circ }$, sedangkan periode $y_2=\sin 5x$ dengan $k=5$ adalah $P_2=\frac{{360}^{\circ }}{5}={72}^{\circ }$.
Dapat disimpulkan bahwa periode $y_1$ sama dengan 5 kali periode $y_2$.
Amplitudo:
Amplitudo $y_1=5\sin x$ dengan $a=5$ adalah $A_1=|a|=|5|=5$, sedangkan amplitudo $y_2=\sin 5x$ dengan $a=1$ adalah $A_2=|a|=|1|=1$. Dapat disimpulkan bahwa amplitudo $y_1$ 5 kali amplitudo $y_2$.
Pernyataan yang benar ada pada pilihan E.

2. Grafik di bawah ini adalah grafik fungsi $\cdots \cdot$

A. $f\left(x\right)=\frac{1}{2}\sin \frac{1}{2}x$
B. $f\left(x\right)=\frac{1}{2}\sin 2x$
C. $f\left(x\right)=\frac{1}{2}\cos 2x$
D. $f\left(x\right)=2\cos \frac{1}{2}x$

Pembahasan

Perhatikan sketsa gambar berikut.

Grafik di atas merupakan modifikasi grafik cosinus (karena grafiknya dimulai dari sumbu-$Y$) dengan bentuk umum $f\left(x\right)=a\cos kx$.
Grafik juga menunjukkan bahwa nilai maksimum fungsinya $\frac{1}{2}$, sedangkan nilai minimumnya $-\frac{1}{2}$, sehingga
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{\frac{1}{2}-(-\frac{1}{2})}{2}=\frac{1}{2}\end{array}$
Saat $x=0^{\circ }$, nilai fungsinya $\frac{1}{2}$, lalu berulang kembali di $x=\pi$, sehingga periodenya $\pi$. Dengan demikian, $k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{\pi }=2$.
Jadi, grafik fungsi di atas adalah grafik fungsi $f\left(x\right)=\frac{1}{2}\cos 2x$

(Jawaban C)E. $f\left(x\right)=2\cos 2x$

3. Grafik dibawah adalah grafik fungsi $\cdots \cdot$

A. $y=2\sin x,0^{\circ }\le x\le {270}^{\circ }$
B. $y=2\cos 4x,0^{\circ }\le x\le {270}^{\circ }$
C. $y=4\sin 2x,0^{\circ }\le x\le {270}^{\circ }$
D. $y=4\cos 2x,0^{\circ }\le x\le {270}^{\circ }$
E. $y=4\sin 4x,0^{\circ }\le x\le {270}^{}$

Pembahasan

Perhatikan sketsa gambar berikut.

Beranjak dari grafik sinus yang memiliki bentuk umum $f\left(x\right)=a\sin kx$, kurva pada gambar tidak bergeser dan berawal dari titik $(0,0)$. Grafik juga menunjukkan bahwa nilai maksimum dan minimum fungsi adalah $4$ dan $-4$, sehingga
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{4-(-4)}{2}=4\end{array}$
Pada saat nilai $x={180}^{\circ }$, fungsi kembali bernilai $0$, lalu berulang kembali seperti sebelumnya, sehingga periodenya adalah ${180}^{\circ }$, dan akibatnya
$k=\frac{{360}^{\circ }}{{180}^{\circ }}=2$
Jadi, rumus fungsi $f\left(x\right)=4\sin 2x$ dengan batas interval $0^{\circ }\le x\le {270}^{\circ }$
(Jawaban C)

4. Perhatikan grafik berikut.

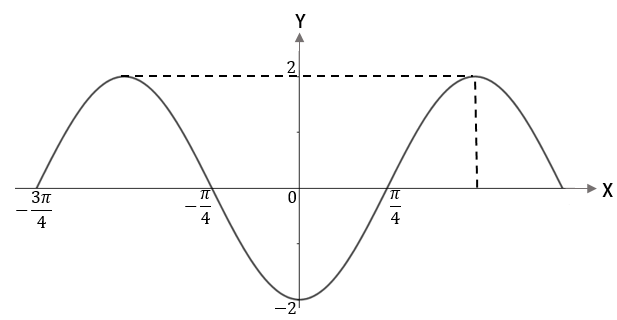
Fungsi yang memenuhi grafik di atas adalah $\cdots \cdot$
A. $f\left(x\right)=-2\sin (x-\frac{\pi }{4})$
B. $f\left(x\right)=-2\sin (x+\frac{\pi }{4})$
C. $f\left(x\right)=-2\sin (2x-\frac{\pi }{2})$
D. $f\left(x\right)=-2\sin (2x+\frac{\pi }{2})$
E. $f\left(x\right)=-2\sin (2x-\frac{\pi }{4}$)

Pembahasan

Beranjak dari grafik sinus: karena kurva bergeser (ke kiri) sejauh $\frac{\pi }{4}$, maka bentuk umum grafik fungsinya adalah $f\left(x\right)=y=a\sin k(x-c)$.
Untuk grafik ini, nilai $c$ yang menentukan pergeseran kurva adalah $-\frac{\pi }{4}$.
Dimulai dari titik $x=-\frac{3\pi }{4}$ yang nilai fungsinya 0, grafik fungsi kembali bernilai $0$ dan berulang kembali di titik $x=\frac{\pi }{4}$, sehingga periode grafik fungsinya adalah $\frac{\pi }{4}–(-\frac{3\pi }{4})=\pi$.
Dengan demikian,
$k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{\pi }=2$
Nilai $a$ ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{2-(-2)}{2}=2\end{array}$
Catatan: Pilihan ganda pada soal menunjukkan bahwa $a=-2$, artinya kurva sinus menurun, lalu menanjak. Ini menjadi alasan mengapa kita anggap kurva bergeser ke kiri.
Jadi, rumus grafik fungsinya adalah$$f\left(x\right)=-2\sin 2(x+\frac{\pi }{4})=-2\sin (2x+\frac{\pi }{2})$$(Jawaban D)

5. Diketahui $f\left(x\right)=\cos x+3$ dengan $0\le x\le 2\pi$. Daerah hasil fungsi $f\left(x\right)$ adalah $\cdots \cdot$
A. $-3\le f\left(x\right)\le 3$              D. $0\le f\left(x\right)\le 3$
B. $-2\le f\left(x\right)\le 2$              E. $2\le f\left(x\right)\le 4$
C. $-1\le f\left(x\right)\le \; 1$

Pembahasan

Agar $f\left(x\right)=\cos x+3$ mencapai maksimum, maka $\cos x$ haruslah sebesar-besarnya, yaitu $\cos x=1$. Untuk itu,
$f_{\text{maks}}\left(x\right)=1+3=4$
Agar $f\left(x\right)=\cos x+3$ mencapai minimum, maka $\cos x$ haruslah sekecil-kecilnya, yaitu $\cos x=-1$. Untuk itu,
$f_{\text{min}}\left(x\right)=-1+3=2$
Jadi, daerah hasil fungsi $f\left(x\right)$ adalah semua nilai (bilangan real) dari $2$ sampai $4$, atau secara matematis ditulis $2\le f\left(x\right)\le 4$
(Jawaban E)

DAFTAR PUSTAKA :

https://mathcyber1997.com/soal-dan-pembahasan-fungsi-trigonometri-dan-grafiknya/

https://markusmatangela.files.wordpress.com/2015/05/modul-matematika-kelas-xi-turunan.pdf