SOAL DAN PEMBAHASANNYA
REMEDIAL PTS
1. Diketahui premis-premis berikut :
Premis 1 : Jika masyarakat membuang sampah pada tempatnya maka lingkungan bersih'
Premis 2 : Jika lingkungan bersih maka hidup akan nyaman.
KESIMPULAN dari 2 premis tersebut adalah Jika masyarakat membuang sampah pada tempatnya maka hidup akan menjadi nyaman.
2. Buktikan dengan induksi matematika bahwa Pn : 1+3+5+7+...+(2n-1) =
bernilai benat untuk setiap n bilangan asli!
Pembahasan :
1 + 3 + 5 + 7 + ... + (2n – 1) = n²
Langkah pertama
Akan dibuktikan untuk n = 1 Benar
(2n – 1) = n²
2(1) – 1 = 1²
2 – 1 = 1
1 = 1 (benar)
Langkah kedua
Misal untuk n = k benar
1 + 3 + 5 + 7 + ... + (2k – 1) = k²
Akan dibuktikan untuk n = (k + 1) juga benar
1 + 3 + 5 + 7 + .... + (2k – 1) + (2(k + 1) – 1) = (k + 1)²
|__________________|
k² + (2(k + 1) – 1) = (k + 1)²
k² + 2k + 2 – 1 = (k + 1)²
k² + 2k + 1 = (k + 1)²
(k + 1)² = (k + 1)²
(Benar)
Jadi TERBUKTI bahwa 1 + 3 + 5 + 7 + ... + (2n – 1) = n² berlaku untuk setiap n bilangan asli.
3. Tunjukan bahwa barisan geometri berlaku
Pembahasan :
4. Buktikan dengan Induksi Matematika bahwa :
1 + 1 + 1 + .... + 1 = n untuk n є N
1+2 2+3 3+4 n(n+1) (n+1)
Pembahasan :
5. Buktikan bahwa semua untuk bilangan asli n, a²ⁿ¯¹ + b²ⁿ¯¹ habis dibagi oleh a+b dengan menggunakan induksi matematika.
1) buktikan kebenaran untuk
(Benar)
2) asumsikan benar untuk
,
( menunjukkan bahwa
merupakan kelipatan 9)
3) cek kebenaran untuk
akan terbukti benar jika habis dibagi 9
bisa buktikan itu dengan induksi lagi
buktikan bahwa habis dibagi 9
1) cek kebenaran untuk
(benar)
2) asumsikan benar untuk
3) cek kebenaran untuk
terbukti bahwa habis dibagi 9 benar
maka pernyataan awal tadi juga benar
7. buktikan untuk masing-masing bilangan asli n ≥ 5 akan berlaku
2n - 3 ＜ 2ⁿ¯²
Pembahasan :
n ≥ 5 = {1,2,3,4,5}
2n - 3 < 2ⁿ¯² = 2(1) - 3 < 2¹¯²
= (-1) < 0 (benar)
2(2) - 3 < 2²−² = 1 < 2 (benar)
2(3) - 3 < 2³￣³ = 3 < 4 (benar)
2(4) - 3 < 2⁴￣² = 5 < 6 ( benar)
2(5) - 3 < 2⁵¯² = 7 < 8 ( benar)
maka pernyataan diatas adalah benar
akann kita gunakan cara eliminasi (menghilangkan dulu) salah satu variabel, kita coba hilangkan x-nya dulu yaa..
persamaan x+2y=4 kita kalikan dengan 2, maka menjadi
2x+4y = 8 -------> (persamaan 1)
2x-3y = -13 ------> (persamaan 2)
--------------- - (dikurangi)
7y = 21
y = 21/7
y = 3
nilai y = 3 kita masukkan kdlam salah satu persamaan di atas, misalkan pada
persamaan x+2y = 4,
x+2.3 = 4
x+6 = 4
x = 4-6
x = -2
jadi penyelesainnya adalah x = -2 dan y = 3
⇒ Kita Buat Tabel Untuk memudahkan:
Model || Polos || Garis || Harga
I || 1 || 3 || 150.000
II || 2 || 1 || 100.000
Stok || 20 || 20 || maksimum
⇒Kita buat kalimat matematika dari Tabel diatas Dengan kain polos sebagai (x) dan kain bergaris sebagai (y) :
x + 2y ≤ 20
3x + y ≤ 20
dengan :
x ≥ 0
y ≥ 0
Dan Fungsi Tujuan adalah harga jual : 150.000x + 100.000y
⇒Tentukan nilai fungsi x dan y pada grafik fungsi :
Dari x + 2y = 20 :
x = 0, y ⇒ 0 + 2y = 20
⇒ 2y = 20
⇒ y = 20/2
⇒ y = 10
Titik Koordinat ⇒ (0,10)
y = 0, x ⇒ x + 2y = 20
⇒ x + 0 = 20
⇒ x = 20
Titik Koordinat ⇒(20,0)
Dari 3x + y = 20
x = 0 , y ⇒ 3x + y = 20
⇒ 0 + y = 20
Titik Koordinat ⇒ (0,20)
y = 0, x ⇒ 3x + y = 20
⇒ 3x + 0 = 20
⇒ 3x = 20
⇒ x = 20/3
Titik Koordinat ⇒ (20/3,0)
Dari Titik - titik tersebut tarik garis lurus hingga terhubung.
Lalu kita cari titik potong dari garis tersebut, dgn metode eliminasi dan subtitusi :
Eliminasi y :
x + 2y = 20 | x 1 | x + 2y = 20
3x + y = 20 | x 2 | 6x + 2y = 40
============ -
-5x = -20
x = 20/5
x = 4
Subtitusikan nilai x pada persamaan 3x + y = 20 :
3 . 4 + y = 20
12 + y = 20
y = 20 - 12
y = 8
Koordinat titik potong garis pada (4,8)
⇒Selanjutnya Dari Titik - titik yang berpotongan kita uji dengan :
Fungsi Tujuan f(x,y) = 150.000x + 100.000y :
Ada 3 titik pada Grafik (perhatikan lampiran)
A. Titik (0,10) = 150.000 . (0) + 100.000 . (10) =
= 0 + 1.000.000 = 1.000.000
B. Titik (4,8) = 150.000 . (4) + 100.000 . (8) =
= 600.000 + 800.000 = 1.400.000
C. Titik (20/3,0) = 150.000 . (20/3) + 100.000 . (0) =
= 1.000.000 + 0 = 1.000.000
Dari Hasil Uji diatas dapat dilihat, penghasilan terbesar pada titik (4,8) yaitu sebesar Rp.1.400.000,00
JADI PENGHASILAN MAKSIMUM YANG DAPAT DI PEROLEH ADALAH Rp.1.400.000,00
diket:
⇒ mencari transpos matrisk A
⇒
⇒ mencari matriks C
⇒ mencari det C
det C = (3)(3) - (-6)(8)
= 9 + 48
det C = 57
Matriks A tidak mempunyai invers
Jadi
|A| = 0
(2x + 1)(5) – 3(6x – 1) = 0
10x + 5 – 18x + 3 = 0
8 – 8x = 0
8 = 8x
x =
x = 1
Saling tegak lurus jika a : b = ...a. -6 : 1
b. -3 : 2
c. 1 : 1
d. 2 : 3
e. 1 : 2
Pembahasan:
Garis g = -2x + ay = 4
Garis h = bx + 3y = 12
mg = 2/a
mh = -b/3
karena g dan h saling tegak lurus, maka mg x mh = -1, maka:
2/a . –b/3 = -1
-2b/3a = -1
2b/3a = 1
3a = 2b
Sehingga a : b= 2 : 3
Jawabannya : D
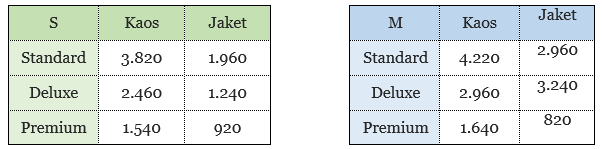
- Sehingga, kita mendapatkan matriks-matriks produksi S dan M sebagai berikut.
- Dari matriks yang diperoleh dari poin 1, kita dapat menghitung banyaknya pakaian yang telah diproduksi oleh pabrik di Surabaya. Banyaknya kaos yang telah diproduksi adalah 7.820, sedangkan banyaknya jaket yang sudah diproduksi adalah 4.120. Selanjutnya, banyaknya kaos yang diproduksi oleh pabrik di Malang adalah 8.820, sedangkan banyaknya jaket yang telah diproduksi adalah 7.020.
- Diketahui perkiraan peningkatan produksinya adalah 4% = 0,04. Artinya, jika n adalah banyaknya produksi pakaian tahun kemarin, maka banyaknya produksi pada tahun ini adalah n + 0,04n = 1,04n. Sehingga, matriks produksi pada tahun depan dapat ditentukan dengan menggunakan perkalian skalar sebagai berikut.
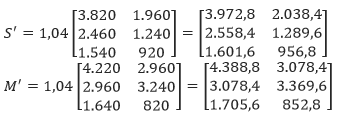
Sehingga dari matriks di atas kita mendapatkan perkiraan banyaknya pakaian yang akan diproduksi oleh JCloth di pabrik Surabaya ataupun Malang. Pabrik di Surabaya akan memproduksi kaos kurang lebih 3.973 kualitas standard, 2.558 kualitas deluxe, dan 1.602 kualitas premium serta memproduksi jaket sebanyak 2.038 kualitas standard, 1.290 kualitas deluxe, dan 956,8 kualitas premium. Sedangkan pada, pabrik di Malang akan memproduksi kaos sebanyak 4.389 kualitas standard, 3.078 kualitas deluxe, 1.706 kualitas premium serta meproduksi jaket sebanyak 3.078 kualitas standard, 3.370 kualitas deluxe, dan 852,8 kualitas premium pada periode yang sama. - Untuk menentukan banyaknya total pakaian yang diproduksi oleh JCloth, kita jumlahkan matriks S’ dengan M’ seperti berikut.
Dari penjumlahan matriks di atas, kita memperoleh informasi banyaknya pakaian yang akan diproduksi oleh JCloth. Dengan menjumlahkan semua elemen-elemen matriks penjumlahan tersebut, kita peroleh bahwa banyaknya pakaian yang akan diproduksi oleh JCloth kurang lebih 28.142.
y = penghapus
5x + 3 y = 11.500 (x2)
4x + 2 y = 9.000 (x3)
_______________
10x + 6 y = 23.000
12x + 6y = 27.000
_______________ (-)
-2x = -4.000
x = 2.000
4x + 2y = 9.000
4*2000 + 2y = 9000
2y = 1000
y = 500
jadi harga pensil = 2000 dan penghapus = 500
sehingga doni harus membayar 6*2000 + 5*500 = 12.000+2.500 = 14.500
Banyaknya makanan disetorkan = A
A =
b. Nyatakan harga makanan dalam bentuk matriks
Harga makanan = B
B =
c. Hitung pemasukan Bu Ani dari setiap kantin dengan cara perkalian matriks
Perkalian Matriks A dan Matriks B
AB =
AB =
Kantin A: Rp. 55.000,00
Kantin B: Rp. 93.000,00
Kantin C: Rp. 100.000,00
d. Carilah determinan matriks dari banyaknya makanan yang disetorkan setiap harinya
|A| = (10 X 15 X 10) + (10 X 8 X 15) + (5 X 20 X 20) - (5 X 15 X 15) - (10 X 20 X 8) - (10 X 8 X 20)
|A| = -100 - 800 + 875
|A| = -15
3x + 4y = 55
Jika ditulis dalam bentuk matriks:
Jadi, Lisa bekerja selama 9 jam sedangkan Muri bekerja selama 7 jam.
No comments:
Post a Comment