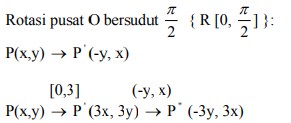1. Ditentukan matriks transformasi .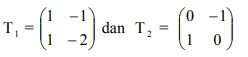 Hasil transformasi titik
Hasil transformasi titik
(2,-1) terhadap T1 dilanjutkan T2 adalah….
A. (-4,3)
B. (-3,4)
C. (3,4)
D. (4,3)
E. (3,-4)
Jawaban : A
Pembahasan :

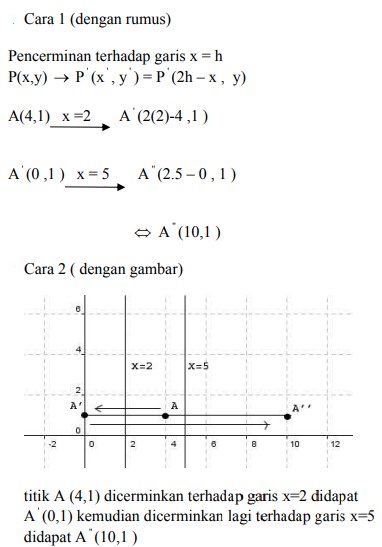
2. Bayangan titik A (4,1) oleh refleksi (pencerminan) terhadap garis x =2 dilanjutkan Refleksi (pencerminan) terhadap garis x = 5 adalah titik….
Pembahasan :
3. Tentukanla bayangan titik P(-6,3) oleh dilatasi terhadap titik pusat O(0,0) dengan faktor skala -1/2 .
Pembahasan:
Dengan demikian, x' = 3 dan y' = -3/2.
Jadi, bayangan titik P(-6,3) oleh dilatasi terhadap titik pusat O(0,0)
dengan faktor skala -1/2 adalah P'(3 , -3/2).
4. Titik A(1 , 2) diputar 30 derajat berlawanan arah dengan arah putaran jarum jam terhadap titik asal O(0 , 0). Bayangan titik A oleh rotasi tersebut ialah ....
A. A'(1/2√3 - 1 , 1/2 + √3)
B. A'(1/2√3 + 1 , 1/2 + √3)
C. A'(1/2√3 - 1 , 1/2 - √3)
D. A'(1/2√3 + 1 , 1/2 - √3)
E. A'(1/2√3 - 1 , √3)
Pembahasan :
Tentukan bayangan titik A:
x' = x cos α - y sin α
x' = 1 cos 30 - 2 sin 30
x' = 1/2√3 - 1
Bayangan titik y:
y' = x sin α + y cos α
y' = 1 sin 30 + 2 cos 30
y' = 1/2 + √3
Makara bayangan A = A'(1/2√3 - 1 , 1/2 + √3)
Jawaban: A
5.Jika titik A(15,8) direfleksikan terhadap 3. 3. Garis x=7, maka bayangan titik A adalah titik A’ dengan koordinat….
Jawaban :
Pembahasan :

6. Diketahui koordinat titik
T(−1,5). Bayangan titik T oleh transformasi yang diwakili oleh matriks (−432−1), dilanjutkan refleksi terhadap garis x=8 adalah ⋯⋅A. T′(30,−7) D. T′(3,−7)B. T′(19,23) E. T′(−3,−7)C. T′(19,−22)Pembahasan :
Bayangan titik T(−1,5) oleh transformasi matriks dapat dinyatakan oleh skema:
T(−15)(−432−1)−−−−−−−→T′[(−432−1)(−15)]=T′(−4(−1)+3(5)2(−1)+(−1)(5))=T′(19−7)Transformasi titik dilanjutkan oleh refleksi terhadap garis x=8 sehingga diperoleh
T′(19−7)Rx=−8−−−→T′′(2(8)−19−7)=T′′(−3−7)
Jadi, koordinat bayangan titik T adalah (−3,−7)
(Jawaban E)
7. Jika persamaan garis lurus
y=2x+3, maka persamaan garis lurus yang dihasilkan oleh translasi T=(3,2) adalah ⋯⋅A. y=3x D. y=2x−4B. y=2x+6 E. y=2x−1C. y=2x−6Pembahasan :
Ambil satu titik yang dilalui garis itu, misalkan titik (x,y). Koordinat bayangan titik ini setelah ditranslasikan oleh T(3,2) ditunjukkan oleh skema panah berikut.
(x,y)T(3,2)−−−→(x+3,y+2)
Dengan demikian, dapat ditulis x′=x+3 dan y′=y+2, atau
{x=x′−3y=y′−2
Substitusikan kedua bentuk ini pada persamaan garis y=2x+3.
y=2x+3y′−2=2(x′−3)+3y′=2x′−6+3+2y′=2x′−1
Jadi, bayangan garis y=2x+3 setelah ditranslasikan oleh T(3,2) adalah y=2x−1
(Jawaban E)
8. Luas bayangan persegipanjang PQRS dengan
P(-1,2), Q(3,2), R (3,-1), S(-1,-1)
karena dilatasi [0,3] dilanjutkan rotasi pusat O bersudut π/2 adalah…
A. 36
B. 48
C.72
D. 96
E. 108
Jawaban : E
Pembahasan :
dilatasi [0,3] :
[O,3k] : P(x,y) → P ‘(3x, 3y)
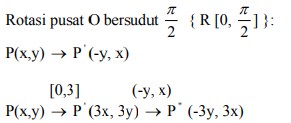
Sehingga :
P(x,y) → P” (-3y, 3x)
P(-1,2), Q(3,2), R (3,-1), S(-1,-1)
P(-1,2) → P” (-6,-3)
Q(3,2) → Q” (-6,9)
R (3,-1) → R” (3,9)
S(-1,-1) → S” (3,-3)
Buat sketsa gambarnya:
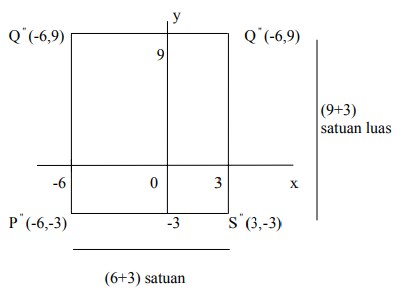
Sehingga luas transformasinya adalah :
Panjang (p) x lebar (l) = 12 x 9 = 108 satuan luas
9. ABCD adalah sebuah persegi dengan koordinat titik-titik sudut A(1,1), B(2,1), C(2,2) dan D(1,2). Tentukan peta atau bayangan dari titik-titik sudut persegi itu oleh dilatasi [O,2]!
Jawaban :
Pembahasan :

10. Perhatikan grafik berikut.
 Salah satu translasi yang dapat memindahkan garis g ke garis l adalah ⋯⋅A. [05] D. [30]B. [0−5] E. [3−4]C. [−50]
Salah satu translasi yang dapat memindahkan garis g ke garis l adalah ⋯⋅A. [05] D. [30]B. [0−5] E. [3−4]C. [−50] Pembahasan :
Secara geometri, kita dapat melakukan translasi pada titik ke titik yang dilalui masing-masing garis tersebut.
Dari titik (−2,0) bergeser 5 satuan ke kanan (+5) menuju titik (3,0) sehingga translasi yang sesuai adalah [50].
Selain itu, bisa juga dari titik (0,4) lalu digeser ke bawah sejauh 4 satuan (−4) dan 3 satuan ke kanan (+3) menuju titik (3,0) sehingga translasi yang sesuai adalah [3−4].
(Jawaban E)
Daftar Pustaka :
https://soalkimia.com/contoh-soal-transformasi-geometri/
https://mathcyber1997.com/soal-dan-pembahasan-transformasi-geometri-tingkat-sma/



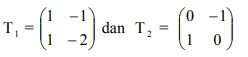 Hasil transformasi titik
Hasil transformasi titik