LUAS DAN VOLUME DAERAH YANG BERKAITAN DENGAN INTEGRAL BERSAMA CONTOH SOALNYA

Jakarta, 6 April 2021

Davin Ilham Wijaya (10)

XI IPS 2

Assalamualaikum semuanya....

Saya akan membahas tentang.........

LUAS DAN VOLUME DAERAH YANG BERKAITAN DENGAN 

INTEGRAL BERSAMA CONTOH SOALNYA

Luas Daerah di Atas Sumbu-x

Luas daerah yang dibatasi kurva y = f(x), sumbu-x, garis 

$x=a$ dan $x=b$

dengan $f\left(x\right)\ge 0$ pada $[a,b]$ adalah :$$L={\int }_a^{b}f\left(x\right)dx$$

Luas Daerah di Bawah Sumbu-x

Luas daerah yang dibatasi kurva y = f(x), sumbu-x, garis $x=a$ dan $x=b$ dengan $f\left(x\right)\le 0$ pada $[a,b]$ adalah : $$L=-{\int }_a^{b}f\left(x\right)dx$$

Luas Antara Dua Kurva

Luas daerah yang dibatasi kurva $y=f\left(x\right)$, $y=g\left(x\right)$, garis $x=a$ dan $x=b$ dengan $f\left(x\right)\ge g\left(x\right)$ pada $[a,b]$ adalah : $$L={\int }_a^b\left(f\left(x\right)-g\left(x\right)\right)dx$$

Volume Benda Putar Terhadap Sumbu-x

Volume benda putar jika daerah yang dibatasi kurva y = f(x), sumbu-x, garis $x=a$ dan $x=b$ diputar 360^o mengelilingi sumbu-x adalah :
$$V=\pi {\int }_a^b{y}^{2}dxatau$$$$V=\pi {\int }_a^b{\left[f\left(x\right)\right]}^{2}dx$$

Volume benda putar jika daerah yang dibatasi kurva y₁ = f(x), y₂ = g(x), garis $x=a$ dan $x=b$ diputar 360^o mengelilingi sumbu-x adalah :$$V=\pi {\int }_a^b\left(y{{}_1}^2-y{{}_2}^2\right)dxatau$$$$V=\pi {\int }_a^b\left({\left[f\left(x\right)\right]}^2-{\left[g\left(x\right)\right]}^2\right)dx$$

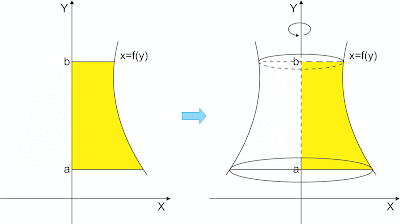
Volume Benda Putar Terhadap Sumbu-y

Volume benda putar jika daerah yang dibatasi kurva x = f(y), sumbu-y, garis $y=a$ dan $y=b$ diputar 360^o mengelilingi sumbu-y adalah :$$V=\pi {\int }_a^b{x}^{2}dyatau$$$$V=\pi {\int }_a^b{\left[f\left(y\right)\right]}^{2}dy$$

Volume benda putar jika daerah yang dibatasi kurva x₁ = f(y), x₂ = g(y), garis $x=a$ dan $x=b$ diputar 360^o mengelilingi sumbu-y adalah :$$V=\pi {\int }_a^b\left(x{{}_1}^2-x{{}_2}^2\right)dyatau$$$$V=\pi {\int }_a^b\left({\left[f\left(y\right)\right]}^2-{\left[g\left(y\right)\right]}^2\right)dy$$

Contoh Soal :

1. Tentukan luas daerah yang diarsir pada gambar di bawah ini!

Pembahasan:
Tentukan batas-batasnya terlebih dahulu.

• Batas kanan:  x√y
• Batas kiri: sumbu y (x = 0)
• Batas atas: y = 9
• Batas bawah: y = 0

Luas daerah yang diarsir adalah
Jadi, luas daerah yang diarsir adalah 18 satuan luas.

2. Tentukan luas daerah yang dibatasi oleh y = x2 – 3x – 10 dengan y = x + 2

Pembahasan:
Berdasarkan soal di atas, terlihat bahwa daerah dibatasi oleh 2 fungsi, yaitu fungsi kuadrat y = x2 – 3x – 10 dan fungsi linier y = x + 2, sehingga berlaku rumus cepat untuk luas.

Substitusikan nilai a, b, dan c yang sudah diperoleh ke dalam persamaan berikut.

Luas daerahnya adalah sebagai berikut.

3. Volume benda putar yang terbentuk jika daerah yang dibatasi oleh kurva $x-y^2+1=0$, $-1\le x\le 4$, dan sumbu-$X$, diputar mengelilingi sumbu-$X$ sejauh ${360}^{\circ }$ adalah $\cdots$ satuan volume.
A. $8\frac{1}{2}\pi$                    D. $12\frac{1}{2}\pi$
B. $9\frac{1}{2}\pi$                    E. $13\frac{1}{2}\pi$
C. $11\frac{1}{2}$

Pembahasan : 

Kurva $x-y^2+1=0$ dapat ditulis menjadi $y^2=x+1$. Bila kita gambar kurvanya yang berupa parabola terbuka ke kanan, beserta garis tegak $x=-1$ dan $x=4$, kita akan memperoleh gambar seperti berikut.
Daerah yang diarsir merupakan daerah yang dibatasi oleh kurva tersebut dan sumbu-$X$ pada selang $[-1,4]$.
Bila diputar mengelilingi sumbu-$X$ sejauh ${360}^{\circ }$, maka kita peroleh
$$\begin{array}{cc}V& =\pi {\int }_{-1}^4{y}^2\text{d}x\\ & =\pi {\int }_{-1}^4(x+1)\text{d}x\\ & =\pi {[\frac{1}{2}{x}^2+x]}_{-1}^4\\ & =\pi [\left(\frac{1}{2}\right(4{)}^2+4)-\left(\frac{1}{2}\right(-1{)}^2+(-1))]\\ & =\pi \left[\right(8+4)-(\frac{1}{2}-1)]\\ & =\pi (12+\frac{1}{2})=12\frac{1}{2}\pi \end{array}$$Jadi, volume benda putar yang terbentuk adalah $12\frac{1}{2}\pi$ satuan volume.
(Jawaban D)

4. Volume benda dari daerah yang dibatasi oleh kurva 

$y=x^2$ dan garis $y=2x$ setelah diputar ${360}^{\circ }$ mengelilingi sumbu-$Y$ adalah $\cdots$ satuan volume.
A. $16\pi$                       D. $2\frac{2}{3}\pi$
B. $8\pi$                         E. $2\frac{1}{3}\pi$
C. $3\frac{2}{3}\pi$

Pembahasan:

Gambarkan sketsa kurvanya terlebih dahulu seperti berikut.

Daerah yang diarsir merupakan daerah yang akan diputar terhadap sumbu-$Y$.
Daerah tersebut terbatas pada absis titik potong kedua kurva dan dapat ditentukan dengan menyamakan kedua fungsinya.
$\begin{array}{cc}y& =y\\ x^2& =2x\\ x^2-2x& =0\\ x(x-2)& =0\end{array}$
Diperoleh $x=0$ atau $x=2$.
Jadi, daerah arsir berada pada selang $[0,2]$.
[diputar terhadap sumbu-$Y$]
$y=x^2\iff x^2=y$
$y=2x\iff x=\frac{y}{2}\iff x^2=\frac{y^2}{4}$
Perhatikan bahwa pada selang tersebut, kurva $y=x^2$ selalu berada di atas kurva $y=2x$ (cara melihatnya: semakin ke kanan, artinya semakin ke atas) sehingga volume benda putar yang terbentuk dinyatakan sebagai berikut.
$\begin{array}{cc}V& =\pi {\int }_0^4(x_1^2-x_2^2)\text{d}y\\ & =\pi {\int }_0^4(y-\frac{y^2}{4})\text{d}y\\ & =\pi {[\frac{1}{2}{y}^2-\frac{1}{12}{y}^3]}_0^4\\ & =\pi \left[\frac{1}{2}\right(4^2-0^2)-\frac{1}{12}(4^3-0^3\left)\right]\\ & =\pi [8-5\frac{1}{3}]=2\frac{2}{3}\end{array}$
Jadi, volume benda putar yang terbentuk sebesar $2\frac{2}{3}$ satuan volume.
(Jawaban D)

Daftar Pustaka:

https://smatika.blogspot.com/2016/09/aplikasi-integral-menentukan-luas-daerah.html

https://smatika.blogspot.com/2016/11/aplikasi-integral-menghitung-volume.html

https://mathcyber1997.com/soal-dan-pembahasan-volume-benda-putar-menggunakan-integral/