MATEMATIKA: INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA

INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA

Jakarta, 23 Maret 2021

Davin Ilham Wijaya (10)

XI IPS 2

Assalamualikum semuanyaa.....

Materi dikesempatan ini kita akan mebahas mengenai

INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA

Pengertian Integral

Pengertian Integral secara sederhana yaitu invers (kebalikan) dari suatu turunan. Penjebaran lebih luasnya adalah sebuah konsep bentuk penjumlahan berkesinambungan dan bersama dengan inversnya.

Sifat Integral

$\int_a^a f(x) \, dx = 0$

$\int_a^b f(x) \, dx = - \int_b^a f(x) \, dx$

$\int_a^b k f(x) \, dx = k \int_a^b f(x) dx$

$\int_a^b (f(x) + g(x)) \, dx = \int_a^b f(x) \, dx + \int_a^b g(x) \, dx$

$\int_a^b (f(x) - g(x)) \, dx = \int_a^b f(x) \, dx - \int_a^b g(x) \, dx$

Jika $a<b<c$ , maka

$\int_a^c f(x) \, dx = \int_a^b f(x) + \int_b^c f(x)$

Harap dicatat ya sifat integral diatas, akan sangat memudahkan nantinya untuk mengerjakan soal.

Jenis Integral

Seperti yang sudah dijelaskan sebelumnya, terdapat 2 Jenis Integral, yaitu: Integral Tak Tentu dan Integral Tentu

Integral Tak Tentu

Integral Tak Tentu adalah pengintegralan fungsi $f(x)$ apabila turunannya telah diketahui.

Integral Tak Tentu Fungsi Aljabar

Rumus

Berikut ini Rumus dari Integral Tak Tentu

$\int f(x) \, dx = F(x) + C$

Keterangan

$f(x)$ = persamaan kurva
$F(x)$ = luasan di bawah kurva f`(x)
$C$ = konstanta

Sifat

Pada integral tak tentu berlaku sifat berikut

$\int ax^n \, dx = \frac{a}{n+1}x^(n+1)+C$

$\int k f(x) \, dx = k \int f(x) dx$

$\int (f(x) + g(x)) \, dx = \int f(x) \, dx + \int_a^b g(x) \, dx$

$\int (f(x) - g(x)) \, dx = \int f(x) \, dx - \int_a^b g(x) \, dx$

Contoh

Berikut ini contoh dari Integral Tak Tentu

$\int (2x+5)dx = 2x^2+5x+c$

$\int (3x-3)dx = x^3-5x+c$

Integral Tak Tentu Fungsi Trigonometri

Pada fungsi trigonometri berlaku integral tak tentu sebagai berikut

$\int cos x \, dx = sin x + C$

$\int sin x \, dx = - cos x + C$

$\int cos(ax+b)dx = \frac{1}{a}sin(ax+b)+C$

$\int sin(ax+b)dx = - \frac{1}{a}cos(ax+b)+C$

Contoh Soal

1. Berikut ini saya bagikan contoh soal beserta jawabannya.
$\int (e^x)^-2 \, dx = ...$
Misal : $u=e^x$
Maka:
$du = e^x \, dx$
$du = u \, dx$
$\frac{1}{u}du=dx$
Jadi,
$\int (e^x)^{-2} \, dx$
$=\int (u)^{-2}.\frac{1}{u}du$
$=\int \frac{1}{u^2}.\frac{1}{u}du$
$=\int \frac{1}{u^3}du$
$=\int u^3 \, du$
$=- \frac{1}{2}u^2+c$
Jadi nilai $u$ adalah
$= -\frac{1}{2}(e^x)^{-2}+c$

2. Selesaikan Integral berikut ini.

$\int 8x^{3x} - 3x^{2x} + x + 5 \, dx$

Jawaban

$=\frac{8x^{3+1}}{3+1}-\frac{3x^{2+1}}{2+1}+\frac{1x^{1+1}}{1+1}+5x+c$
$=\frac{8x^{4}}{4}-\frac{3x^{3}}{3}+\frac{x^2}{2}+5x+c$
$=2x^4-x^3+\frac{1}{2}x^2+5x+c$

3. Selesaikan Integral berikut ini.

$\int (2x + 1) (x - 5) dx$

Jawaban

$\int 2x^2+x-10x-5+C$
$\int 2x^2+9x-5+C$
$\int \frac{2}{3}x^3+\frac{9}{2}x^2-5x+C$

4. Tentukan hasil dari ʃ 3x2 dx

Pembahasan :

Jadi, hasil dari ʃ 3x2 dx adalah x3 + C.

5. Carilah nilai dari ʃ (3x-2)(x+6) dx

Pembahasan :

(3x-2)(x+6) = 3x2 + 18x – 2x -12 = 3x2 + 16x -12

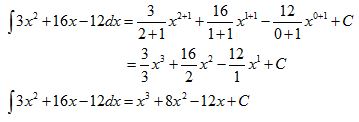
Contoh Soal Integral no 4

Jadi, hasil dari ʃ (3x-2)(x+6) dx adalah x3 + 8x2 – 12x + C.

Sekian pembahasan materi kali ini, semoga bermanfaat dan STAY SAVE, Terimakasihhhhh

Daftar Pustaka :

https://www.edura.id/blog/matematika/integral/

https://rumuspintar.com/integral/contoh-soal/

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)