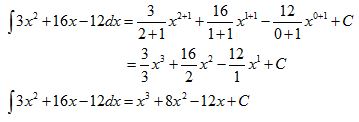INTEGRAL TERTENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA

Jakarta, 30 Maret 2021

Davin Ilham Wijaya (10)

XI IPS 2


Assalamualaikum.....

Yuk.... mari kita bahas tentang...

INTEGRAL TERTENTU BERSAMA SIFAT-SIFATNYA 

BESERTA CONTOH SOALNYA


Pengertian Integral Tentu 

Integral tentu adalah integral yang memiliki nilai batas atas dan batas bawah. Batas-batas yang diberikan umumnya adalah suatu nilai konstanta. Namun dapat juga batas-batas tersebut berupa variabel. Untuk mencari nilai integral tertentu dari suatu fungsi, pertama kita substitusikan batas atas ke dalam fungsi hasil integral, kemudian dikurangi hasil substitusi batas bawah pada fungsi hasil integral.

Secara matematis dapat ditulis sebagai berikut:
Keterangan:
f(x) = fungsi yang nantinya akan kita integralkan
d(x) = variabel integral
a = batas bawah pada variabel integral
b = batas atas pada variabel integral
F(a) = nilai integral pada batas bawah
F(b) = nilai integral pada batas atas

Sifat-sifat pada Integral Tentu 

Integral sebenarnya dapat ditentukan dengan mudah. Untuk mempermudah perhitungan integral, perhatikan sifat-sifat integral berikut ini.

Pertama. Jika batas atas dan batas bawah dalam suatu integral tentu adalah sama, maka hasil integral tentu dari fungsi tersebut akan sama dengan nol karena tidak ada daerah antara batas batas tersebut.

Berikut ini adalah rumus secara matematis:
Kedua. Jika batas atas dan batas bawah dalam integral tentu diubah posisinya (batas atas menjasi batas bawah dan batas bawah menjadi batas atas) untuk fungsi integral yang sama, maka akan diperoleh hasil hasil yang sama namun berbeda tanda.

Berikut ini adalah rumus secara matematis:
Ketiga. Jika f(x) adalah fungsi integral dan k merupakan tetapan (konstanta) sembarang.

Berikut ini adalah rumus secara matematis:
Keempat. Misalkan diberikan dua buah fungsi yaitu f(x) dan g(x), maka integral  tentu dari penjumlahan atau pengurangan kedua fungsi tersebut dapat diselesaikan.
Berikut ini adalah rumus secara matematis:
Kelima. Misalkan terdapat dua integral dengan nilai fungsi yang sama dan nilai pada batas atas pada fungsi pertama sama dengan nilai pada batas bawah pada fungsi kedua.

Berikut ini adalah rumus secara matematis:
Keenam. Apabila fungsi f(x) nya bukan suatu fungsi melainkan konstanta.

Berikut ini adalah rumus secara matematis:

Contoh - Contoh Soal 

Soal 1
Hitunglah hasil dari integral tentu berikut ini
A. ¾
B. ⅘
C. ⅜
D. ⅔
E. 4/3
Jawab:
Mathematics
Maka jawabannya adalah A

Soal 2
Tentukan hasil integral dari fungsi berikut:
A. 20
B. 30
C. 10
D. 40
E. 50
Jawab:








Maka jawabannya adalah B

Soal 3
Tentukan hasil integral dari fungsi berikut:




A. 4
B. 5
C. 6
D. 7
E. 8
Jawab:







Maka jawabannya adalah C.

Soal 4
Tentukan hasil integral dari fungsi berikut ini:




A. 80√2
B. 82√2
C. 84√2
D. 80√3
E. 84√3
Jawab:










Maka jawabannya adalah E.


Soal 5
Tentukan hasil dari integral pada fungsi berikut ini.




A. 124/4
B. 123/4
C. 125/2
D. 124/2
E. 126/4

Jawab:
Mathematics













Maka jawabannya adalah A.


Daftar Pustaka:
https://www.sheetmath.com/2018/06/integral-tentu-contoh-soal-dan-pembahasan.html
By at No comments:

INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA

Jakarta, 23 Maret 2021

Davin Ilham Wijaya (10)

XI IPS 2


Assalamualikum semuanyaa.....

Materi dikesempatan ini kita akan mebahas mengenai  

INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA


Pengertian Integral
Pengertian Integral secara sederhana yaitu invers (kebalikan) dari suatu turunan. Penjebaran lebih luasnya adalah sebuah konsep bentuk penjumlahan berkesinambungan dan bersama dengan inversnya.






Sifat Integral

\int_a^a f(x) \, dx = 0

\int_a^b f(x) \, dx = - \int_b^a f(x) \, dx

\int_a^b k f(x) \, dx = k \int_a^b f(x) dx

\int_a^b (f(x) + g(x)) \, dx = \int_a^b f(x) \, dx + \int_a^b g(x) \, dx

\int_a^b (f(x) - g(x)) \, dx = \int_a^b f(x) \, dx - \int_a^b g(x) \, dx

Jika a<b<c, maka

\int_a^c f(x) \, dx = \int_a^b f(x) + \int_b^c f(x)

Harap dicatat ya sifat integral diatas, akan sangat memudahkan nantinya untuk mengerjakan soal.

Jenis Integral

Seperti yang sudah dijelaskan sebelumnya, terdapat 2 Jenis Integral, yaitu: Integral Tak Tentu dan Integral Tentu

Integral Tak Tentu

Integral Tak Tentu adalah pengintegralan fungsi f(x) apabila turunannya telah diketahui.

Integral Tak Tentu Fungsi Aljabar

Rumus

Berikut ini Rumus dari Integral Tak Tentu

\int f(x) \, dx = F(x) + C

Keterangan

f(x) = persamaan kurva
F(x) = luasan di bawah kurva f`(x)
C = konstanta


Sifat

Pada integral tak tentu berlaku sifat berikut

\int ax^n \, dx = \frac{a}{n+1}x^(n+1)+C

\int k f(x) \, dx = k \int f(x) dx

\int (f(x) + g(x)) \, dx = \int f(x) \, dx + \int_a^b g(x) \, dx

\int (f(x) - g(x)) \, dx = \int f(x) \, dx - \int_a^b g(x) \, dx

Contoh

Berikut ini contoh dari Integral Tak Tentu

\int (2x+5)dx = 2x^2+5x+c

\int (3x-3)dx = x^3-5x+c

Integral Tak Tentu Fungsi Trigonometri

Pada fungsi trigonometri berlaku integral tak tentu sebagai berikut

\int cos x \, dx = sin x + C

\int sin x \, dx = - cos x + C

\int cos(ax+b)dx = \frac{1}{a}sin(ax+b)+C

\int sin(ax+b)dx = - \frac{1}{a}cos(ax+b)+C


Contoh Soal

1. Berikut ini saya bagikan contoh soal beserta jawabannya.

\int (e^x)^-2 \, dx = ...
Misal : u=e^x
Maka:
du = e^x \, dx
du = u \, dx
\frac{1}{u}du=dx
Jadi,
\int (e^x)^{-2} \, dx
=\int (u)^{-2}.\frac{1}{u}du
=\int \frac{1}{u^2}.\frac{1}{u}du
=\int \frac{1}{u^3}du
=\int u^3 \, du
=- \frac{1}{2}u^2+c
Jadi nilai u adalah
= -\frac{1}{2}(e^x)^{-2}+c

2. Selesaikan Integral berikut ini.

\int 8x^{3x} - 3x^{2x} + x + 5 \, dx

Jawaban

=\frac{8x^{3+1}}{3+1}-\frac{3x^{2+1}}{2+1}+\frac{1x^{1+1}}{1+1}+5x+c

=\frac{8x^{4}}{4}-\frac{3x^{3}}{3}+\frac{x^2}{2}+5x+c

=2x^4-x^3+\frac{1}{2}x^2+5x+c

3. Selesaikan Integral berikut ini.

\int (2x + 1) (x - 5) dx

Jawaban

\int 2x^2+x-10x-5+C

\int 2x^2+9x-5+C

\int \frac{2}{3}x^3+\frac{9}{2}x^2-5x+C

4. Tentukan hasil dari ʃ 3x2 dx 

Pembahasan :









Jadi, hasil dari ʃ 3x2 dx adalah x3 + C.

5. Carilah nilai dari ʃ (3x-2)(x+6) dx
Pembahasan :

(3x-2)(x+6) = 3x2 + 18x – 2x -12 = 3x2 + 16x -12

Contoh Soal Integral no 4

Jadi, hasil dari ʃ (3x-2)(x+6) dx adalah x3 + 8x2 – 12x + C.



Sekian pembahasan materi kali ini, semoga bermanfaat dan STAY SAVE, Terimakasihhhhh



Daftar Pustaka :
https://www.edura.id/blog/matematika/integral/
https://rumuspintar.com/integral/contoh-soal/







By at No comments:
Subscribe to: Posts (Atom)